Quotations
Thought for Us
Imagination takes you everywhere
A. Einstein
****************************************************************
Invitation to serve as MRS session chair
To Sun Bo <sun.bo@sz.tsinghua.edu.cn> on 2021-11-05 04:16
Thank you for the opportunity to present:
"Near-field Heat Transfer by Quantum Mechanics"
at the November Meeting.
However, I have a problem!!!
A few days ago, I was informed of having prostrate cancer.
Therefore, I am requesting that my live PPT presentation be a Vimeo video.
https://vimeo.com/642645515
Just enter the URL in a PC browser online. Have Zoom show you how to share during meeting.
I would be available in-person to answer questions.
Thomas Prevenslik
Near-Field Radiative Heat Transfer
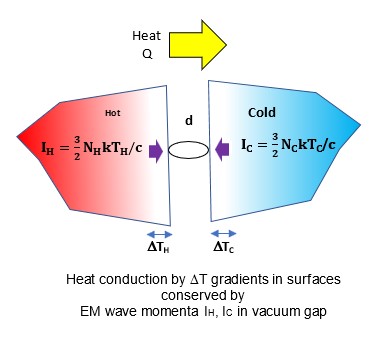
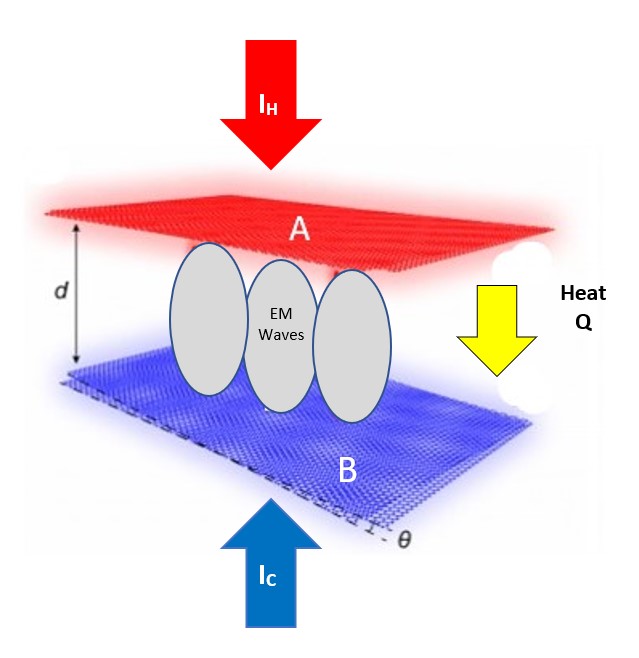
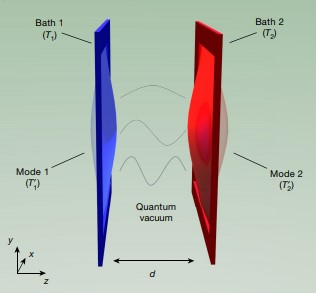
Near-fiield heat radiative transfer (NFRHT) is based on the classical Fluctuation Dissipation Theorem that requires the heat produced in macroscopic bodies upon absorbing EM radiation creates temperature fluctuations that is reciprocated by temperature fluctuations producing EM radiation. But NFRHT in nanoscale gaps between hot and cold bodies is governed by quantum mechanics (QM) and not classical physics. Indeed, the Planck law precludes temperature fluctuations in nanoscale gaps upon absorbing heat. However, all known NFRHT theories are based on the difference of surface temperatures of nanoscale gaps. In effect, the Planck law requires theories of NFRHT that do not depend on temperature which means all known NFRHT theories are invalid.
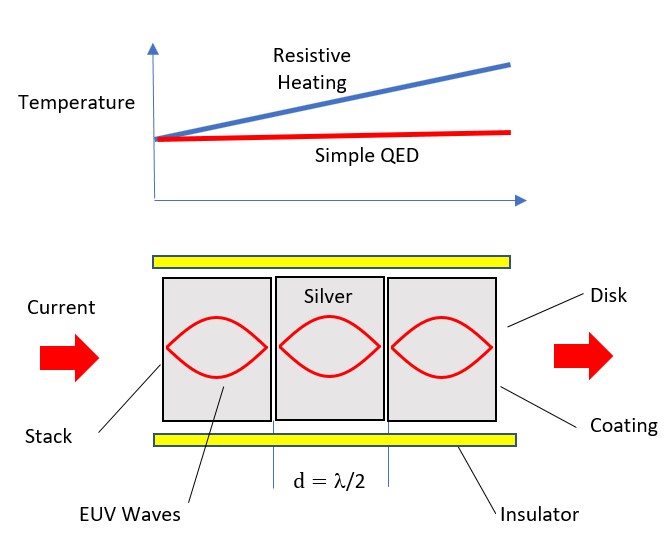
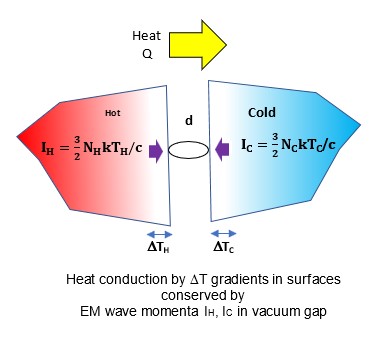
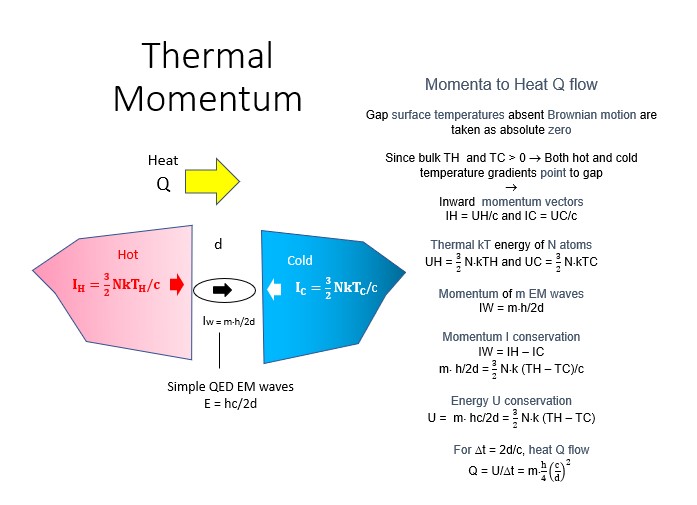
One temperature independent NFRHT theory is simple QED based on the Planck law that conserves heat by creating temperature independent EM standing or travelling waves across the evacuated nanoscale gaps. But the heat requires EM confinement across the gap to a half-wavelength having the dimension d of the gap. In simple QED, the EM confinement is provided by the momenta of the thermal energy of the in the heat flow between hot and cold bodies, the hot and cold momenta directed toward their gap surfaces because of the thermal gradient formed with gap surface temperatures at absolute zero, the absolute zero temperatures because the Planck law requires Brownian motion to cease. Heat flows if the hot momentum exceeds the cold momentum.
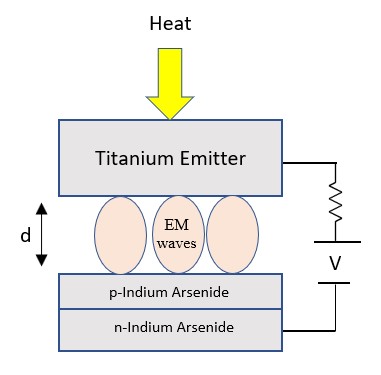
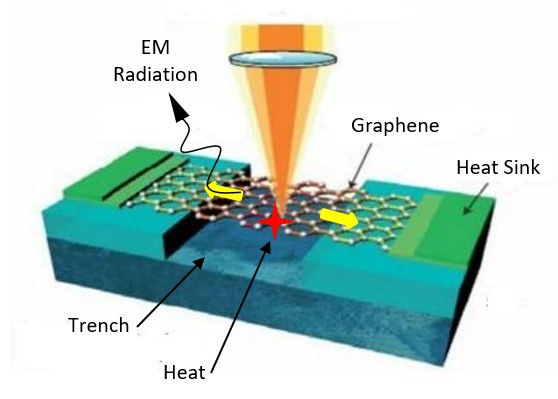
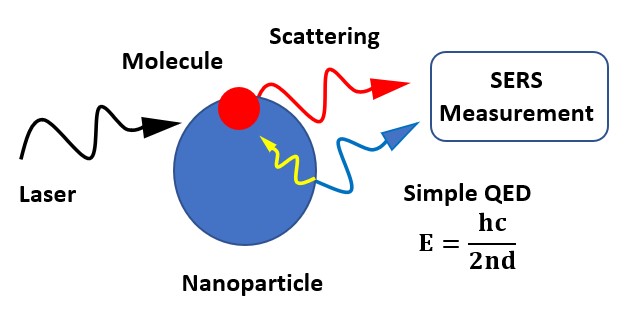
Simple QED highlights the stark difference between QM and classical physics illustrated by the emission of bright white-light from a Joule heated single graphene layer (0.337 nm) over a nanoscale trench reported in the literature.
The application of NFRHT to the nanoscale trench is difficult to implement as the Joule heat from the graphene layer into the nanoscale trench is not known. Instead, the Fourier equation was applied to the graphene layer assuming Joule heating produces electron temperatures of 2800 K giving graphene temperatures near 2000 K. But bright-white light may require higher temperatures, say up to 5000 K. In contrast, simple QED argues the graphene remains at ambient temperature. Instead, 1.8 keV soft X-rays are produced across the graphene thickness that fluoresce down to about 200 eV, the heat of which is either lost to the surroundings or enters the trench, the latter by simple QED creating IR waves standing in the trench, the overtones of the IR producing the observed bright white-light absent high temperatures. Consistent with simple QED, the graphene does not acquire 2800 K electron temperatures evidenced by the observation of white-light at 10 K. Indeed, there is a stark difference between QM and classical physics and should be expected whenever classical physics including NFRHT is used to explain observations at the nanoscale.
See Video
Superconductivity by Simple QED
Almost a century ago, Cooper theorized a pair of electrons in a positive-charged metal lattice containing free electrons could attract each other by electron–phonon interaction, the phonon being the collective motion of the positively-charged lattice. The attraction only required a small binding energy of 10−3 eV, but thermal energy would rapidly break the pair which required lattice temperatures approaching absolute zero in order to allow a significant number of Cooper pairs to exist to explain superconductivity. But this is questionable as a crystal lattice near the ground state at absolute zero lacks the temperature necessary to even create phonons. Later, Bardeen suggested the exciton (electron-hole pairs) mechanism of electron attraction instead of phonons. In a sandwich structure consisting of alternate thin layers of metal and semiconductors, the metal electrons would tunnel into the semiconductor to form excitons that provide electron attraction. To this day, electron attraction by exciton mechanisms remains complex. In contrast, simple QED induced zero resistance instead of superconductivity is self-evident from first principles. Simple QED is a nanoscale heat transfer theory based on the Planck law of quantum mechanics (QM) that conserves heat with EM radiation instead of temperature. Hence, simple QED avoids the Cooper pair requirement of lattice temperatures approaching absolute zero by conserving attendant Joule heating by EM radiation which at EUV levels ionizes the silver lattice atoms and increases the free electrons to approach zero resistance in compensating for Joule heat. In effect, simple QED replaces superconductivity at absolute zero by zero resistance at ambient temperature. Only valid at the nanoscale, simple QED is applied to a nanowire comprising a stack of 200 nm diameter silver disks along the wire length, the disk thickness corresponding to the 82 nm half-wavelength of the 7.57 eV ionization potential of silver, the stack housed in an insulative evacuated tube. Separate circuits are provided for wire ionization and use of the wire in the nano electronic application. An alternative nanowire design is presented comprising a stack of 100 nm spherical silver nanoparticles (NPs).
Conclusions
Superconductivity based on Cooper pairs that form from the attraction between free electrons in an electrical conductor by the interaction with phonons is questionable as phonons only exist at finite temperatures - not anywhere near absolute zero.
Electron attraction by exciton (electron-hole pairs) allowing the possibility of superconductivity at ambient temperature. However, producing the excitons using thin films is difficult, unless the photoelectric effect can be somehow implemented in superconductivity.
In this regard, superconductivity by simple QED differs from Cooper pairs produced by phonons or excitons as the focus shifts from achieving zero resistance at absolute zero to accepting the resistance at ambient temperature while converting the respective Joule heat to EUV radiation that ionizes the silver disks to increase the current flow offsetting resistance losses.
Simple QED is a nanoscale heat transfer process based on the Planck law that denies atoms in nanostructures the heat capacity to conserve heat by an increase in temperature. Instead, conservation proceeds by converting heat to EM radiation.
To illustrate superconductivity by simple QED, a nanowire is presented comprising a stack of 200 nm diameter - 82 nm thick silver disks in an evacuated insulative tube. The disk thickness is selected to be the half-wavelength of the first silver ionization potential, the Joule heat produced in the disk converted to EUV radiation that carries the current through the nanowire as an EM wave, the analysis of which is self-evident.
Similar to Joule heat QJ producing EUV radiation across the disk thickness, simple QED was proposed as an alternative to chemiosmosis which is based on complex chemical reactions in converting adenosine diphosphate (ADP) to adenosine triphosphate (ATP). Mitochondria using body heat Q naturally produces UV in the 50-100 nm spaces between cristae. In this way, ATP is directly synthesized from ADP by UV in the presence of phosphor in the mitochondria avoiding the complex sequential chemical reactions of chemiosmosis.
The work in this paper is a preliminary study. The work is ongoing. Modifications of the nanowire design are reported when made.
A preliminary Papers available.
Cosmic Dust Redshift
Over the past century, Hubble's redshift of light from galaxies has intrigued scientists to ponder the current expansion rate of the Universe. Recently, a young schoolgirl published an article on the expansion of the Universe that illustrates how the mis-interpretation of redshift of galaxies has falsely led astronomers over a century are being passed on to future generations.
Indeed, the redshift of galaxies thought to support Hubbell's expansion of the Universe is nothing more than the redshift of a spectral line (SL) emitted from a galaxy upon interacting with nanoscopic cosmic dust. What this suggests is the Universe is not and never was expanding, nor does dark matter exist.
Analysis is presented for the redshift of Balmer-lines over a range of silicate dust nanoparticle (NP) diameters. The interaction of the SL photon with the NP is by the simple QED method of nanoscale heat transfer that based on the Planck law denies the atoms in the NP the heat capacity to conserve the absorbed SL photon by an increase in temperature.
In this regard, the NP diameter is required to be smaller than the SL photon wavelength which spontaneously immerses the NP in SL radiation. But the SL radiation cannot penetrate the NP surface as NP temperatures do not exist for Fourier conduction. Conservation may only proceed by creating temperature independent EM waves.
At this instant, the redshifted SL photon is created.
The Planck energy of the redshifted SL photon define as the Planck constant divided by the time for the EM wave to travel across and back the NP diameter. EM confinement of SL photon energy within the NP is provided by the inwardly disposed momentum of the SL radiation itself.
Redshift in cosmic dust occurs when the wavelength of the simple QED photon is greater than that of the incident SL photon, and may accumulate in many successive NP interactions before reaching the observer on Earth. Blueshift does not occur because more energy is required than available in the incident single SL photon.
Conclusion
For a century, Astronomy has been misdirected by cosmic dust to false notions of an expanding Universe and dark matter neither of which exist and can never be verified experimentally. Sadly, young scientists are nevertheless being guided to continue the false notions of an expanding Universe and dark matter into the next century.
See Paper
Solar UV Treatment of Covid-19 by Nanoparticles
In mid-2020, simple QED showed Moderna's mRNA delivered to the cell in lipid NPs cell would be inactivated, or at least degraded by the UV produced by the NP itself. What this means is the mRNA has nothing to do with the high > 90% efficacies of the Covid-19 vaccines. Therefore, the UV from NPs alone is somehow eliciting Covid-19 immunity.
A NP treatment was proposed whereby only Covid-19 patients tested positive having the live virus in their bodies would be treated to avoid vaccination of the entire world population. The UV emission from NPs only needs to inactivate a few virions in the patient that then act as the antigen to elicit Covid-19 immunity for inactivating the remaining virus in their body. However, the high efficacy of Moderna for patients tested negative suggests NP induced UV efficacy has nothing to do with the patient having Covid-19 virions in his body. Other mechanisms that use the UV emission from NPs were reviewed.
In mid-2021, solar UV was considered based on correlations between the distribution of COVID-19 cases and deaths and the amount of solar at the Earth's surface. Observations of the cumulative solar UV exposure have quantified the amount of radiation available e.g., for pre-vitamin D3 synthesis or SARS-CoV-2 inactivation by sunlight. While the statistical outcomes do not give a specific cause-effect relationship, the presence of the vitamin D3 in the skin suggest immunomodulatory effects on the innate and adaptive immune systems.
In this regard, the NP treatment of Covid-19 was revised based on solar UV converting 7-DHC in the skin to Vitamin D3 consistent with showing > 90% of Covid-19 deaths correlated by Vitamin D deficiency.
Unlike Covid-19 virions which are in ultra-low concentration in the bloodstream even in patients tested positive, the UV from NPs over the very large area of skin of all patients is far more likely to explain Moderna’s > 90% efficacy. For purposes of illustration, the NPs are depicted larger than the capillaries in the above figure. NPs are far smaller than capillary diameters of 5 microns..
Specifically, the NPs im the blood emit UV to synthesize 7-dehydrocholesterol (7-DHC) in basal epidermis [2] to produce Vitamin D3 which is converted in the liver into 25(OH)D the circulating metabolite. The kidneys convert 25(OH)D into bioavailable 1,25(OH)2D promoting immune regulatory T cells. Vitamin D protects against infectivity from COVID-19 and deficiency in 25(OH)D is correlates with positive Covid-19.
The press release PR
Second law and Near Field Radiative Heat Transfer
Near-field Radiative Heat Transfer (NFRHT) assumes heat Q flow across vacuum nanoscale gaps follows Rytov's theory of electrodynamic fluctuations in deriving gap surface temperatures. However, the Planck law of quantum mechanics (QM) is shown to preclude heat from producing temperature fluctuations in nanoscale gaps surfaces.
Absent Brownian motion, atoms in both hot and cold gap surfaces approach absolute zero which suggests a violation of the Second law of Thermodynamics (SLT) as it is not possible to transfer heat between reservoirs having the same hot and cold temperature. Indeed, the Carnot statement of the SLT gives the efficiency of a thermodynamic cycle to depend solely on the difference between hot and cold reservoir temperatures, the efficiency vanishing for gap surfaces having the same temperature suggesting heat Q flow is not possible.
The Planck law requires NFHRT theories to be independent of temperature. One such NFRHT theory is simple QED that carries heat Q flow across the gap by EM waves. Simple QED is shown to satisfy the SLT as the gap surface atoms at absolute zero create thermal gradients with adjacent atoms having finite kT energy to conduct heat from both hot and cold surfaces into the gap. But in the gap, the Fourier law is no longer valid meaning the conductive heat is conserved by creating the momenta of hot and cold EM waves, the difference in EM momenta carrying the heat Q flow across the gap.
The SLT is not violated as the bulk temperatures of hot and cold EM momenta correspond to Carnot reservoirs, even though the gap surface temperatures are identical. Simple QED is illustrated for thermophotovoltaic devices having a nanoscale gap between the thermal emitter and PV cell.
Conclusions
The SLT is not violated in nanoscale gaps even though gap surfaces have identical temperatures approaching absolute zero as required by the Planck law.
Carnot's hypothesis on the impossibility of converting heat to work at a single temperature, and that heat flow requires to have thermal reservoirs with different temperature are both based on the classical limit that does not apply to the nanoscale at the quantum limit.
Heat is transferred by Fourier conduction from both hot and cold atoms having finite kT energy along thermal gradients with gap surface temperatures approaching absolute zero.
At the gap surface, the hot and cold conductive heat is conserved with the momenta of hot and cold EM waves, the difference of which carries the heat across the gap, thereby satisfying the SLT even though gap surface temperatures are identical.
PVT devices comprising nanoscale vacuum gaps between the emitter and PV cell producing enhanced heat Q flow based on NFRHT theory of temperature fluctuations is invalid by the Planck law which denies gap surface atoms the heat capacity necessary for temperature fluctuations.
Experiments to verify NFRHT in nPVT based on temperature fluctuations are perhaps near impossible as the Planck law denies temperatures to fluctuate in nanoscale gaps. Measurements reported in the literature of temperature differences across nanoscale gaps are fraught with error as the difference in gap surface temperatures sought simply do not exist.
Only temperature independent NFRHT theories for nTPV devices are valid in nanoscale gaps, one of which is simple QED based on the Planck law itself.
Simple QED applied to experimental data of an InAs nPVT device shows a slight peaking in heat Q flow at temperatures < 665 K at the 3.5 micron bandgap wavelength λ of the PV cell, but for λ < 3.5 microns, the heat Q flow increases 40-fold, the latter considered invalid.
NFRHT based on Rytov's fluctuation theory does not predict zero heat Q flow, and therefore contact of gap surfaces is used. But then, the Q flow is thought to increase by conduction even though the temperatures are the same.
Unlike NFRHT, simple QED allows zero heat Q/N flow without contact at the same gap surface temperatures. Based on EM waves, the heat QH/N supplied to a gap d is required to satisfy QH/N > Q/N = h(c/d)^2/4 as otherwise the wave cannot form and Q = 0.
By simple QED, zero nTPV heat flow Q in vacuum gaps between emitter and PV cell may be assumed up to peaking at the bandgap wavelength λ of the PV cell. Hence, simple QED suggests setting the gap d = λ/2.
Since nTPV bandgaps are in the NIR, 60 nm gaps producing λ = 2d = 120 nm EM radiation in the EUV is not expected to enhance efficiency above that of NIR nTPV devices.
Simple QED usually applied to nanoscale gaps d < 100 nm is extended to nTPV devices having gaps d < 3 microns as NIR radiation is > 250 times more likely to conserve heat Q flow than an increase in temperature.
A preliminary Paper is available.
Near-Field Thermophotovoltaics with Nanoscale Gaps
Near-field thermophotovoltaics (nTPV) are thought to enhance thermoelectric efficiency by separating the emitter and PV cell by nanoscale gaps.
Experimental verification of nTPV is difficult, and instead, support of concept relies on Near-field Radiation Heat Transfer (NFRHT) analysis based on Rytov's theory of fluctuation temperature. But in nanoscale gaps, the Planck law denies atoms the heat capacity necessary for temperature fluctuations.
What this means is nTPV lacks even a theoretical basis. In effect, the Planck law requires a nTPV theory that does not depend on temperature. One such theory is simple QED based on the Planck law that describes nTPV by temperature independent EM travelling waves that carry heat flow by EM waves.
Application of simple QED to a nTPV device with a 60 nm gap between emitter and InAs PV cell with a bandgap wavelength λ = 3.5 microns suggests no enhancement of nTVP efficiency with a slight enhancement at a gap of 1.75 microns. Instead of a 60 nm gap, the nTPV efficiency can be significantly enhanced by setting the gap at 1.75 microns to be resonant with the 3.5 microns InAs bandgap. Regardless, the emitter temperature should be increased to obtain a high efficiency.
Conclusions,
Near-field PVT devices comprising nanoscale vacuum gaps between the emitter and PV cell producing enhanced heat Q flow based on NFRHT theory of temperature fluctuations is invalid by the Planck law which denies gap surface atoms the heat capacity necessary for temperature fluctuations.
Experiments to verify NFRHT in nPVT devices based on temperature fluctuations are perhaps near impossible as the Planck law denies temperatures to fluctuate in nanoscale gaps. Measurements reported in the literature of temperature differences across nanoscale gaps are fraught with error as the difference in gap surface temperatures simply do not exist.
Only temperature independent NFRHT theories for nTPV devices are valid in nanoscale gaps, one of which is simple QED based on the Planck law itself.
Simple QED applied to experimental data of an InAs nPVT device shows a slight peaking in heat Q flow at temperatures < 665 K at the 3.5 micron bandgap wavelength L of the PV cell, but for λ < 3.5 microns the heat Q flow increases 40-fold, the latter not expected.
NFRHT based on Rytov's fluctuation theory does not predict zero heat Q flow, and therefore contact of gap surfaces is used. But then, the Q flow is thought to increase by conduction even though the temperatures are the same.
Unlike NFRHT, simple QED allows zero heat Q flow without contact at the same gap surface temperatures. Based on EM waves, the heat QH supplied to a gap d is required to satisfy QH > Q = h(c/d)^2/4 as otherwise the wave cannot form and Q = 0.
By simple QED, zero nTPV heat flow Q in vacuum gaps between emitter and PV cell may be assumed up to a peaking at the bandgap wavelength λ of the PV cell. Hence, simple QED suggests setting the gap d = λ/2.
Since nTPV bandgaps are in the NIR, 60 nm gaps producing λ = 2d = 120 nm EM radiation in the EUV are not expected to enhance efficiency above that of standard nTPV devices.
Simple QED usually applied to nanoscale gaps d < 100 nm is extended to nTPV devices having gaps d < 3 microns as NIR radiation is > 250 times more likely to conserve heat Q flow than an increase in temperature.
A preliminary Paper is available.
The Planck law cancelled?
Currently, the cancel culture in the USA driven by identity politics threatens not only the traditions of the USA as a country, but also the future of Science. Groups of scientists have placed their perception of Science above those of traditional values, the perceptions of which have consequences.
Over the past decades, the consequence of US scientists canceling the Planck law of quantum mechanics (QM) at the nanoscale in favor of classical physics has led to countless numbers of meaningless papers in the literature returning science to the dark ages at the exorbitant expense of the US taxpayer. Contrary to classical physics that allows atoms at the nanoscale to fluctuate in temperature, the Planck law denies atoms the heat capacity for temperature fluctuations.
What this means is all known theories of Near-Field Radiation Heat Transfer (NFRHT) based on temperature fluctuations in nanoscale gap surfaces are invalid. In effect, the Planck law requires NFRHT theories that do not depend on temperature. One such theory is simple QED based on the Planck law that describes NFRHT by temperature independent EM travelling waves that carry heat flow, the EM waves by the photoelectric effect producing a plasma that increases heat flow. A similar photoelectric argument to refute quantum fluctuations in the attractive Casimir force was made over a decade ago.
Conclusions,
NFRHT theory is based on the falsity that temperatures fluctuate in evacuated nanoscale gaps contrary to the Planck law that denies gap surface atoms the heat capacity necessary for temperature fluctuations.
All known NFRHT theories assume temperature fluctuations in gaps and implicitly require temperature differences between gap surfaces are therefore invalid by the Planck law.
Only temperature independent near-field theories are valid at the nanoscale, one of which is simple QED based on the Planck law itself.
Evanescent waves and phonons on the surface of macroscopic bodies do not exist in the surfaces of nanoscale gaps.
The Planck law aside, NFRHT touted as the method to show the Planck blackbody heat transfer is an unnecessary effort as simple thought experiments on rods with a nanoscale gap does not increase the heat flow along its length.
Experiments to verify NFRHT based on temperature fluctuations are perhaps near impossible as the Planck law denies temperatures in nanoscale gaps. Measurements reported in the literature of temperature differences across nanoscale gaps which do not exist are shown to be fraught with error.
The Casimir effect by charging of plates by the simple QED induced photoelectric effect and not by quantum fluctuations is related to NFRHT by ionizing the gap surfaces, but is not significant for NFRHT micro W heat flows Q.
The Science acceptance of NFRHT theory based on Rytov's fluctuational electrodynamics from classical physics does not bode well for the future of nanotechnology as cancelling the Planck law is a step back into the dark ages
White Light from Nanothermometers
Laser induced white light (WL) spectra of a graphene ceramic based on temperatures far less than Planck's theory of black-body radiation suggested the opening of a band-gap in graphene by multiphoton ionization.
The difficulty is the WL spectra has nothing to do with graphene. Rather, the WL spectra is emission of 30-150 nm Er+3 - Y2O3 nanoparticles (NPs) used as thermometers encrusted in the graphene to measure temperature. The Er+3 spectra is shown to closely match that of the measured graphene ceramic spectra.
Even so, the Er+3 spectra cannot be related to temperature as the theory of simple QED based on the Planck law precludes the NPs of any material from having the heat capacity to increase in temperature upon absorbing heat. Instead, heat from any source excites the WL emission - not temperature. What this means is the long held notion of inferring temperatures from intensity I of emission spectra as noted in the above equation has no physical meaning. Nanothermometers measure HEAT - not temperature. Indeed, the Planck law places in question the validity of temperature measurement by nanothermometers.
Conclusions,
Graphene alone absent a band-gap cannot produce WL.
WL observed from graphene ceramics is caused by encrusted Er+3 - Y2O3 NPs thought to act as nanothermometers to measure graphene temperature.
The emission from NPs of Er+3 - Y2O3 has nothing to do with the temperature of the graphene as temperatures are precluded at the nanoscale by the Planck law.
The long thought notion that CW laser excitation is up-converted in NPs to higher energy photons by questionable additions of multi-photons is superseded by simple QED.
Depending on NP diameter and refractive index, simple QED may red or blue shift the frequency of absorbed CW laser excitation to photons having Planck energy E = hc/λ and wavelength λ = 2nd.
A preliminary Paper is available. Another note on the invalidity of temperature measurements by nanothermometers is given on this nanoqed.org website at page 2020.
Near-field Heat Transfer by the Planck law
The history of near-field heat transfer in nanoscale gaps between macroscopic bodies is based on the Rytov's Fluctuation Dynamics which assumes heat produces temperature fluctuations consistent with classical physics. But under the EM confinement in nanoscale gaps, the Planck law of quantum mechanics precludes temperature fluctuations. Nevertheless, all known near-field heat transfer theories are based on the difference of surface temperatures of nanoscale gaps.
In effect, the Planck law requires theories of near-field heat transfer that do not depend on temperature. One such theory is simple QED formulated based on the Planck law and conserves heat by creating temperature independent EM waves across the nanoscale gap. To highlight the difference between classical physics and quantum mechanics, simple QED is applied to the white light emitted by graphene. Classical physics predicts the white light is produced at 2000 K temperatures in a graphene layer over a nanoscale trench even though bright white light may require 5000 K temperatures. In contrast, simple QED claims the graphene remains at ambient temperature, and instead 1.8 keV soft X-rays are produced across the graphene thickness that then fluoresce down to ~ 270 eV, the heat of which is converted to IR waves standing in the nanoscale trench. The white light is produced by the overtones of the IR waves at ambient temperature instead of 5000 K as suggested by classical physics.
Conclusions,
Current near-field theories are invalid by the Planck law while experimental data is explained by temperature independent standing EM waves consistent with simple QED.
The Planck law refutes Rytov's temperature fluctuations at the nanoscale.
All known near-field heat transfer theories assume temperature fluctuations in gaps and that implicitly require temperature differences between gap surfaces are invalid by the Planck law.
Only temperature independent near-field theories are valid at the nanoscale, one proposal of which is simple QED based on the Planck law itself.
.
A 10minute Video is available including a slightly longer Video comparing a NP with near-field gap are also available.
White light from Graphene by Quantum Mechanics
Near-field heat transfer in nanoscale gaps assumes the atom has kT heat capacity in stark contrast to the Planck law of quantum mechanics (QM) that requires temperature fluctuations to vanish. Since all known near-field theories assume temperature fluctuations, no valid near-field theories exist today.
The Planck law shows the heat capacity of a body depends on the EM confinement wavelength of the constituent atoms given by the EM wave standing or travelling across the body. Classical physics based on macroscopic bodies with long wavelengths allows the atom upon absorbing heat to increase the temperature of the body. However, the Planck law applied to nanoscopic bodies having submicron wavelengths differs significantly from classical physics by denying the constituent atoms the heat capacity to increase in temperature.
In this paper, the difference between classical physics and the Planck law is illustrated for Joule heated white light (WL) emission from a single atom graphene layer at ambient temperature suspended over a nanoscale trench. Classical physics based on the Fourier law gives temperatures of about 1800 K, but WL requires temperatures as high as 5000 K.
But high temperatures are questionable as WL is observed with the graphene layer maintained at 10 K. In this regard, the theory of simple QED nanoscale heat transfer based on the Planck law shows that single layer graphene remains at ambient temperature by conserving Joule heat by emitting soft X-rays into the trench. But like the graphene layer, the nanoscale trench cannot increase in temperature, and instead creates standing IR waves, the overtones of which produce the WL.
Conclusions,
Near-field heat transfer assumes heat produces temperature fluctuations in nanoscale gaps which is refuted by the Planck law that denies atoms in gap surfaces the kT heat capacity to conserve heat by temperature fluctuations.
All known near-field heat transfer theories assume temperature fluctuations in gaps and implicitly require temperature differences between gap surfaces are therefore invalid by the Planck law.
Only temperature independent near-field theories are valid at the nanoscale, one proposal of which is simple QED waves explicitly based on the Planck law.
Temperatures do not exist in suspended single atom graphene layers.
Simple QED conserves Joule heat by creating 1.8 keV soft X-rays across the 0.337 nm graphene layer thickness that fluoresce down to ~ 270 eV.
Like the graphene layer, the nanoscale trench cannot conserve the soft X-ray heat by an increase in temperature, and instead creates the IR waves standing between the graphene layer and the trench bottom.
The WL is a mix of the higher overtones of the fundamental IR standing wave.
Heat Transfer by Momentum of Thermal Energy
Over the past half-century, research in near-field heat transfer across nanoscale gaps based on temperature fluctuations suggests the heat transfer is orders of magnitude greater than the BB limit. But this is unlikely based on the following argument. Consider a 1-D rod with applied heat Q across a nanoscale gap d illustrated below.
Heat Q along the rod from hot TH and cold TC temperatures is not expected to increase across the vacuum gap unless the gap is a source of heat which it is not. The problem is the temperature of the gap surfaces is not known and cannot be measured as nanoscale temperature probes do not exist. Because of this, the gap surface temperatures were assumed to be the same as bulk TH and TC temperatures. Calculations assuming surface temperatures TH and TC using temperature fluctuation theories showed the heat Q flow higher than the BB limit.
High heat Q flow induced by temperature fluctuations in the gap is highly questionable as the Planck law of quantum mechanics precludes the atoms in the gap surfaces from having the heat capacity to produce temperature fluctuations. Indeed, Brownian motion ceases and the surface temperatures effectively approach absolute zero. What this means is evanescent waves and plasmons of any kind that depend on temperature therefore do not exist to be mechanisms of near-field heat transfer. Since all known near-field theories of heat transfer are based on temperature fluctuations, all near-field theories today are invalid. In effect, the Planck law requires non-thermal mechanisms to carry heat Q across the gap.
One such near-field mechanism is simple QED, a nanoscale heat transfer process that conserves heat Q with EM waves across the gap.
The simple QED process is illustrated as follows.
Simple QED gives the EM energy E of the wave, E = hc/2d having momentum IW = m h/2d, where m is the number of waves. Thermal kT energy UH and UC of the hot and cold bodies is transferred across the gap by momenta IW = IH - IC = (UH - UC)/c, the IH and IC momenta both directed to the respective gap surfaces by temperature gradients with gap surfaces approaching absolute zero. Here, the thermal energy U transferred, U =UH - UC = 1.5 N k (TH-TC), where N is an arbitrary number of atoms in both bodies having kT energy. Hence, the energy U transferred is,
U = IW*c = m*hc/2d = 1.5 Nk(TH - TC)
The heat Q transferred is, Q = U/dt , where dt is the time for the half-wave to travel across and back the gap d, dt = 2d/c. Hence, the heat Q,
Q = m*h/4 (c/d)^2.
The momentum transfer from atoms having thermal kT energy differs from conventional heat transfer which only considers momentum transfer of mass in Newton's law for the convection of fluids. In contrast, simple QED argues heat Q flow absent mass is still energy U moving across the gap at light speed c having momentum I = U/c.
Comments are solicited.
Near-field Heat Transfer in Twist Bilayer Graphene
Near-field heat transfer assumes that since EM radiation upon absorption in a body produces temperature fluctuations then temperature fluctuations produce EM radiation, as heat alone producing EM radiation without temperature fluctuations is excluded.
Contrarily, the Planck law precludes heat from producing temperature fluctuations in nanoscale gaps and surfaces. However, all known near-field theories are based on the unverifiable assumption that bulk temperatures exist at gap surfaces. In effect, the Planck law requires theories of near-field heat transfer that do not depend on gap surface temperatures, one such theory described herein is simple QED that conserves heat across gaps by EM waves.
Current twisted bi-layer graphene (tBLG) theories based on temperature fluctuations report the heat transferred is 5 orders of magnitude higher than the blackbody BB limit for twist angles of only a few degrees. In contrast, simple QED shows heat is conserved across nanoscale gaps and comparison with the BB limit is meaningless, i.e., adding a nanoscale gap to a 1-D rod does not increase the heat flow along its length.
The validity of simple QED depending on the EM confinement wavelength of the atom based on the Planck law is supported at cryogenic temperatures well known to shift the Planck law to long wavelengths allowing the near-field at the nanoscale at 300 K to be extended to the macroscale in 50-micron gaps at 15 K.
Importantly, heat flow in nanoscale gaps above the BB limit does not mean actual heat flow is enhanced, but rather only heat flow is conserved across the gap by EM waves - not temperatures. Since all near-field theories based on temperature fluctuations in nanoscale gaps are invalid by the Planck law, future near-field research should be directed to temperature independent theories.
Conclusions,
In nanoscale gaps, the Planck law denies the existence of temperature fluctuations, plasmons, polaritons, evanescent waves, and variants thereof.
All known near-field heat transfer theories based on temperature dependent fluctuations in gaps and temperature differences between gap surfaces are invalid by the Planck law.\
Only temperature independent near-field theories are valid at the nanoscale, one such theory is simple QED explicitly based on the Planck law.
Simple QED conserves heat flow across tLBG gaps while temperature fluctuation theory increases heat flow by 5 orders of magnitude above the BB limit. Small tLBG twist angles cause Moire' fringes between layers, but Moire' fringes are not likely to increase heat transfer across the gap by 10 orders of magnitude.
The size dependent gap validity in simple QED known a half-century ago allowing near-field effects to be observed in macroscopic gaps was assessed by considering the shift in the Planck law to longer wavelengths at cryogenic temperatures. At 15 K, simple QED conserves heat flow but temperature fluctuation theory predicts a 4 order of magnitude increase in heat flow above the BB limit.
Experiments of near-field effects should report the power P delivered at each gap size as temperature alone is not sufficient to show nanoscale gaps do not increase actual heat flow.
Characteristic Radiation
Over a half-century ago, Perel'man predicted latent heat in the transition from vapor to condensate would be carried away by EM radiation called characteristic radiation (CR). More recently, CR was extended to the removal of latent heat of condensation of water vapor on a cooled metal surface that showed IR radiation beyond blackbody radiation was produced that could be construed as unknown spectral lines of water. Condensates are also related to the yet unknown mechanism by which clouds absorb solar radiation in the VIS.
In this paper, simple QED - a nanoscale heat transfer process based on the Planck law that conserves heat by EM radiation instead of temperature - is shown to confirm CR is produced from the latent heat condensing water droplets < 5 microns which means the unexplained IR lines are anomalous having nothing to do with the quantum states of the water molecule. Also, the < 5 micron drops explain the atmospheric VIS absorption thought missing in climate models as the redshift of VIS light to the near IR meaning the VIS is not missing, but rather atmospheric the IR absorption is overstated.
Conclusions
The PeTa theory of IRCR emission at < 20 microns from condensing water vapor is consistent with simple QED, although limited to < 10 microns to allow EM radiation to conserve latent heat by IRCR from < 5 micron water drops instead of the classical increase in temperature.
Perel'man's prediction of conserving latent heat by EM radiation without temperature change is a valid phenomenon.
The VIS absorption in atmospheric physics is not missing, but rather redshift in < 5 m cloud drops to the IRCR emission. Instead, the near IR is overstated.
A Paper is available
T
The in vivo NP Treatment
The CDC approach to the Covid-19 virus was to quickly develop a vaccine which even if successful in the near term would be impossible to implement for the ~8 billion people in the world, let alone unacceptable because of attendant social unrest and economic collapse. I
In mid-2020, a new approach for Covid-19 and other viruses called the Nanoparticle Treatment was proposed targeting only a relatively small number of patients who tested positive for the virus. Messenger mRNA and antigens of the virus having unknown side effects were excluded. Only injections of biodegradable lipid nanoparticles (NPs) in saline are used with the antigen being the actual live Covid-19 virus in the tested positive patient that is inactivated by the UV radiation emitted from the NPs.
The UV is produced by the simple QED theory based on the Planck law which denies atoms in NPs the heat capacity to conserve heat by an increase in temperature, and instead heat from the surroundings is conserved by creating EM radiation at a wavelength depending on the NP size, e.g., 80 nm lipid NPs emit UVC (254 nm) radiation.
In the manner of an in vivo vaccine, the NP treatment uses UVC to inactivate the live Covid-19 virus in the patient to produce the inactivated virus that acts as the antigen to elicit immunity to current and future Covid-19 infections. By controlling the NP dose, the UVC is held to low levels of collateral DNA damage allowing recovery by DNA repair systems that evolved during the UV intense primitive Earth.
*************************************** Epilog ***********************************************
To this day, the pharmaceutical industry (Pfizer/BioNtech, Moderna, AstraZeneca, etc.) is obviously not aware UV radiation is naturally produced in NPs. Historically, NP induced UV in vaccines was present since the 1920's, the NPs located at the periphery of micron-sized alum adjuvants. However, the mechanism by which NPs emit UV had to await simple QED formulated a century later as described by the NP Treatment.
Today, the CDC emphasis on vaccines is devoid of the fact that NPs shown necessary in avoiding fragmentation of mRNA and DNA passing through the cell wall also produce UV that inactivates or at least degrades the mRNA or DNA before ever reaching the cell. In a vaccination, mRNA and DNA carried in NPs is non-workable.
What this means is the > 90% efficacy reported for Covoid-19 vaccines has nothing to do with mRNA or DNA, but rather is caused by the UV produced by the NPs alone. Indeed, only injections of NPs in saline embodied in the NP treatment are necessary for Covid-19. In Covid-19 vaccines, the UV ionizes the mRNA or DNA carried in the NP that then acts as the antigen recognized by the immune system to elicit immunity, but the idea that the efficacy is caused by mRNA or DNA decoding the Covid-19 is erroneous.
Regardless, NPs in Covid-19 vaccines also cause DNA damage to neurons that induce neurological symptoms, and therefore offer no advantage over the NP Treatment, and are only more costly because of mRNA and DNA and attendant storage at cold temperatures.
In conclusion, Covid-19 vaccines have in effect proved the NP Treatment does work, but requires continued CDC and FDA vigilance of limits on NP dosage to avoid problems of UV induced neurological and pulmonary blood clotting.
See Abstract and Video Presentation
Covid-19 fueled by Cytokine Storms?
Instead, the Covid-19 is thought fueled by cytokines comprising interlukins IL-4, IL-6, IL-10, IL-13 as shown in the above figure. See: Is COVID-19 Fueled by a Cytokine Storm? on the web.
However, the cytokines must somehow be created which requires an energy source. Simple QED proposes the Covid-19 itself creates UVB radiation in conserving by the thermal energy of the surroundings - the UVB fuels the cytokine storm.
Conclusions
The nanoscale Covid-19 virus emits EM radiation at a wavelength depending on its diameter and refractive index. Similarly, Covid-19 vaccines deliver mRNA and DNA to the cell in nanoscale carriers of NPs and Ads that also emit EM radiation.
The AstraZeneca Ad vector that delivers DNA to the cell is predicted by simple QED to emit UVB radiation which is well known to activate cytokines to induce blood clots. But the UVB emission depends on the size distribution of Ads which is not available in the public domain. Moreover, the quality control of Ads sizes is required as AstraZeneca uses different manufacturers. Since only specific countries like Norway and Finland have reported serious blood clotting, perhaps the Ad size distribution in the batch delivered is the problem with reported clotting. The FDA should impose tight controls on both Ad and NP size in vaccines.
The CDC is requested to confirm the simple QED prediction of UVB emission from Covid-19 virions, lipid NPs, and adenovirus Ad virions. Spectroscopy is suggested for each entity in water. The samples are placed in UV transparent cuvettes and EM radiation measured with a UV-VIS spectrometer. The only heat required is that of the water at ambient temperature.
A preliminary Paper is available.
Bright White Light from Graphene
The history of near-field heat transfer in nanoscale gaps between macroscopic bodies is based on the Fluctuation Dissipation Theorem (FDT) that requires heat upon absorption of EM radiation to produces temperature fluctuations which means temperature fluctuations can produce EM radiation. But under EM confinement, the Planck law precludes temperature fluctuations in nanoscale gaps which heat may be conserved by creating EM radiation. However, all known near-field heat transfer theories are based on the difference of surface temperatures of nanoscale gaps. In effect, the Planck law requires theories of near-field heat transfer that do not depend on temperature.
One such theory is simple QED that was formulated based on the Planck law and conserves heat by creating temperature independent EM standing waves across the nanoscale gap. Current near-field theories are discussed in relation to simple QED with applications relevant to graphene including: hyperbolic plasmons, super-Planckian radiation, and bright VIS light.
The application of bright VIS emission is notable in that under electrical fields, current near-field theory claims 2000 K temperatures are produced in a graphene layer over a nanoscale trench, but bright white light requires 5000 K temperatures illustrated in the figure below..
Jn contrast, simple QED claims the graphene remains at ambient temperature, and instead soft X-rays are produced across the graphene thickness, the heat of which excites overtones of standing EM waves in the trench to produce bright white light. Current near-field theories are shown invalid by the Planck law while experimental data is explained by temperature independent standing EM waves consistent with simple QED.
Conclusions
The FDT assumes that because EM radiation produces heat with temperature fluctuations then temperature fluctuations can produce EM radiation.
But the Planck law precludes heat from EM radiation creating temperature fluctuations in nanoscale gaps which means the FDT is not applicable and heat may only create EM radiation at the nanoscale.
All known near-field heat transfer theories assume temperature fluctuations in gaps and implicitly require temperature differences between gap surfaces are invalid by the Planck law.
Only temperature independent near-field theories are valid at the nanoscale, one proposal of which is simple QED based on the Planck law itself.
Hyperbolic phonons and evanescent waves valid on the surface of macroscopic bodies do not exist in the surfaces of nanoscale gaps.
Electric field induced 2000 K temperatures do not exist in suspended single atom graphene layers. Instead, Joule heat is conserved by creating soft X-rays across the layer thickness, the heat of which is then conserved by creating the fundamental of EM waves standing between the graphene layer and the bottom of the trench. The white light is a mix of the higher VIS overtones of the fundamental EM standing wave
Graphene: High Thermal Conductivity at the Nanoscale?
Over the last decade, the high thermal conductivity of graphene flakes and carbon nanotube (CNTs) at the nanoscale has received much attention in the heat dissipation of microelectronic devices. But Molecular Dynamics (MD) and Finite Element Models (FEM) analysis in support of high thermal conductivity based on classical physics are no longer valid at the nanoscale because the atoms in nanostructures are assumed to have temperature, when in fact the Planck law denies atoms at the nanoscale the heat capacity to conserve heat by an increase in temperature.
Indeed, phonons dependent on temperature implicit in MD and FEM analysis do not even exist at the nanoscale.
In this regard, the simple QED method of nanoscale heat transfer based on the Planck law conserves heat by the emission of EM radiation instead of increases in temperature. Under steady laser heating at the center of a graphene flake, the in-plane thermal conductivity assumed proportional to the laser heat is highly overstated as soft X-ray emission normal to flake is not included as a significant heat loss. Similarly, most heat in CNTs is dissipated across the diameter making thermal conductivity based on heat transfer along the length also highly overstated.
In contrast, the thermal conductivity of silicon nanowires (NWs) is not measured by assuming heat only flows along the NW length, but rather simply measures the temperature difference across the wire length, the consequence of which is the thermal conductivity of silicon at the nanoscale is not higher than bulk, but rather at least 100X lower than bulk consistent with simple QED.
Conclusions
The Planck law denies atoms in graphene layers the heat capacity to conserve heat across the thickness by an increase in temperature. Phonons depending on temperature do exist along the length of a few microns, but not through the < 1 nm graphene layer.
Simple QED based on the Planck law conserves heat Q across graphene layers by the emission of EM radiation at ~ 280 eV soft X-ray levels.
Assuming laser heat is conducted in-plane to the heat sinks is false as virtually all heat is loss by soft X-rays before ever reaching the sinks. MD and FEM programs ANSYS and ABAQUS based on classical physics are not valid at the nanoscale.
High thermal conductivity of graphene at the nanoscale does not exist as assuming all laser heat flows in-plane through the layer to heat sinks is invalid. In fact, the ETC of graphene layers vanishes in the same way as for silicon NWs.
The 100X lower thermal conductivity of silicon NWs at the nanoscale compared to bulk is determined experimentally by measuring the temperature difference across the wire length. Graphene experiments should do the same.
A preliminary Paper is available.
Simple QED: The Absorption in Raman Scattering?
Simple QED is a nanoscale heat transfer process in nanoparticles (NPs) that conserves absorbed heat with the emission of EM radiation. Incident light having a wavelength greater than the NP diameter imparts an inwardly disposed spherical Poynting vector of momentum that heats the NP surface. Sub-surface penetration of surface heat requires thermal conduction in the NP, but cannot proceed as the Planck law precludes the NP conserving heat by an increase in temperature. Instead, the NP surface heat acts the EM confinement to conserve the heat by creating non-thermal standing EM radiation inside the NP having a half-wavelength equal to the NP diameter. Once the momentum of the accumulated EM radiation exceeds the momentum of the incident light, the NP emits the standing EM radiation to the surroundings at a frequency depending on the NP diameter, a process similar to absorption in Raman scattering.
Conclusion
Simple QED heat transfer in NPs is similar to inelastic Raman scattering with absorption allowing the emission frequency to increase or decrease depending on size de-pendent quantum states of the NP.
A preliminary Abstract and Mp4 video Presentation are available.
Simple QED in Spintronics
Spin-valves comprising alternating nanoscale layers of ferromagnets (FMs) separated by mon-magnetic (NM) spacers are generally thought to produce parallel electron-spins that lower the giant magneto-resistance (GMR) of the disordered state, the change in resistance allowing data storage in magnetic recording.
The picture above shows the GMR of spins in adjacent FMs to be naturally anti-parallel with high electrical resistance. But applying a magnetic field causes an abrupt lowering of the GMR. But is a magnetic field necessary?
Almost a decade ago, the author showed lowering of the GMR was not caused by spin, but rather by EM radiation induced by conserving Joule heat from the electrical current writing and reading in the recording, the EM radiation at UV levels by photoelectric charging the FM and significantly lowering the GMR.
Since then, the theory of simple QED induced heat transfer at the nanoscale has been advanced to prompt the instant updated version of spin consistent with other simple QED applications. Having mothing to do with Feynman's QED, simple QED is based on the Planck law that denies the atoms in FMs under nanoscale EM confinement the heat capacity to conserve Joule heat by an increase in temperature, and instead the heat is conserved by creating non-thermal EM waves standing across the FM layer.
The EM radiation has sufficient Planck energy to ionize FM layers and create excitons (holon and electron pairs) that act as charge carriers to significantly lower the GMR by the dramatic decrease in the resistance of the FM layers even approaching super-conductivity at ambient temperature.
Conclusions:
The Planck law denies atoms in FM layers the heat capacity to conserve heat by an increase in temperature. Phonons depending on temperature do not exist in in FMs which means heat transfer occurs by simple QED induced EM radiation.
Simple QED based on the Planck law conserves heat in the FM layer by the prompt creation of standing EM radiation beyond the UV that promptly ionizes the FM to form holons that lower the GMR.
FMs that demagnetize on a sub- picosecond time scale (< 350 fs) is consistent with simple QED induced heat transfer at the nanoscale.
Simple QED requires brief EM confinement of the heat to produce non-thermal EM waves standing across the FM layer. TIR was used in the early paper, but EM confinement of the standing EM waves is updated here to the inward impulsive momentum of thermal kT radiation from external regions to the FM layer having temperature.
The simulations of simple QED induced switching from writing to reading for the 100 nm layer showed 90% GMR lowering compared to the 22% in the experiment. But simple QED assumed 100% conversion of Power to excitons. Since there are many FM layers stacked on top of each other, 100% conversion of heat to excitons may be justified.
A preliminary Paper is available.
Phonons leap across nanoscale gaps ?
Physics Today report of heat transfer across nanoscale gaps based on phonons mediated by the Casimir effect or quantum fluctuations of electromagnetic fields are assessed in relation to the simple QED theory of nanoscale heat transfer. Simple QED based on the Planck law denies atoms in nano structures and gap surfaces the heat capacity to conserve heat by an increase in temperature with conservation proceeding by the creation of non-thermal EM waves standing across the gap.
Only a single simple QED photon is necessary to explain the experiment, and therefore phonon heat transfer mediated by the Casimir effect is relatively insignificant. Further, the thermal kT energy of atoms in gap surfaces vanishes under EM confinement which means phonons that depend on temperature do not exist in the nanogap surfaces to transfer heat by leaping across the vacuum gap.
Even the Casimir force in the phonon heat transfer theory is questionable. Over a decade ago, the Casimir effect was shown to have nothing to do with quantum fluctuations, but rather caused by photoelectric charging of the plates by simple QED induced EM waves standing across submicron gaps.
See preliminary Paper
The Nanoparticle Treatment and Vaccinations
Traditionally, vaccine development requires years of development and testing, but with the Covid-19 pandemic a rapid response is required as attendant lockdowns and quarantines cause social unrest and potential World economic collapse. However, the CDC did not have a plan in place for a rapid treatment of the Covid-19 or any other unknown viral pandemic because of the focus on preventive vaccines. Nevertheless, Pfizer/BionTech and Moderna rapidly coded the mRNA for the Covid-19 spike protein not only in a short time, but the vaccines also showed 95% efficacy. Since viral vaccines only have efficacies of about 50%, the reason for the high mRNA efficacy was linked to the nanoparticle (NP) carriers not expressed in other vaccines. Early on, encapsulating the mRNA in fatty lipid NPs was found to resolve the breaking apart of the mRNA molecule upon entering the cell. Moderna and others were reported to have used ~ 80 nm NPs, but encapsulated mRNA in NPs created another problem.
The simple QED theory of nanoscale heat transfer predicted the ~ 80 nm NPs produce low levels of ultraviolet (UVC) radiation upon conserving body heat that alters the mRNA before ever reaching the cell. Indeed, UVC is known to induce non-coding RNA that opposes the encoded protein, and therefore the coded Covid-19 spike protein cannot the reason for the high efficacy of the mRNA vaccines. Rather, the 95% efficacy reported for mRNA vaccines is more likely caused by the NP induced UVC modifying the spike protein coding to a lower level coding similar to that of the ancestor of the spike protein that evolved under the intense UVC that existed on the early Earth.
In mid-2020, the author proposed the NP treatment to BARDA based on the UVC from injections of ~ 80 nm NPs in saline, but only for patients tested positive for Covid-19 thereby avoiding the vaccination of the entire World population. Moreover, the UVC in the NP treatment only needs to inactivate a few of the viruses in the patient to produce the antigens necessary to elicit the immunity to inactivate the remaining viruses in the patient as well as any future Covid-19 infections. Clearly, the NP treatment based on NPs alone is inexpensive compared to mRNA vaccines and the difficulties of cold storage are avoided. Later, the delivery by NP injection is expected to be replaced by NP inhalers.
In contrast, the AstraZeneca vaccine is not based on mRNA in lipid NPs, but rather on the larger ~100 nm adenovirus NPs that carry a genetically engineered spike protein in cell cultures into the cells, although at a lower efficacy of 70% because the larger adenovirus NP emits UVB instead of UVC.
In this paper, the simple QED theory based on the Planck law is used to support UVB and UVC radiation from NPs in Covid-19 vaccines, the NP atoms of which lack the heat capacity to conserve heat by an increase in temperature, and instead convert body heat into UVB and UVC.
However, both UVB and UVC may cause collateral DNA damage in the brain leading to the neurological symptoms of Covid-19 now being observed probably because the NP dosage is too high. By controlling the NP dose; however, the UV can be held to low levels allowing recovery of DNA damage over time by natural DNA repair systems. Although the NP treatment was proposed for Covid-19 about a year ago, the problem with the vaccination paradigm in lacking a prompt response to future viral infection pandemics has not gone away. The NP treatment, or the like, offers a simple, inexpensive, and direct method of producing UV radiation to elicit immunity for all known and yet unknown viruses.
The CDC is recommended to begin a test program on the NP treatment to establish the minimum NP dosage that elicits Covid-19 immunity, but also reduces the UVB and UVC induced neurological symptoms observed today, e. g., allergic reactions, loss of smell, headaches, Bell's palsy, etc. including pulmonary symptoms of UVB induced bleeding from toes, etc.
See Abstract
Nanowire Thermal Conductivity
Indeed, phonons do not even exist at the nanoscale, but photons do, as illustrated by EM emission of light from a NW in the above figure.
In contrast, the simple QED method of nanoscale heat transfer based on the Planck law conserves heat in NWs by the emission of EM radiation instead of increases in temperature. Under steady heat flow, EM waves as non-thermal photons stand across the NW diameter and length that partition the heat in term of dissipation time or inverse of standing wave frequencies. In this paper, the simple QED heat transfer response of silicon NWs is compared with experiment and phonon-based derivations of thermal conductivity of NWs at ambient temperatures from 1 to 300 °K.
Conclusions
The Planck law denies atoms in silicon NWs the heat capacity to conserve heat by an increase in temperature. Phonons depending on temperature do not exist in NWs. Non-Fourier nanoscale heat transfer models of NWs based on phonons are highly questionable.
Simple QED based on the Planck law conserves heat by the emission of EM radiation. At temperatures < 300 °K, photons instead of phonons carry the heat at the nanoscale consistent with ballistic models
NWs generally thought to reduce heat flow along the wire length are the consequence of most Joule heat being emitted from the wire cross-section as EM radiation into the surroundings. Only a small fraction of Joule heat is loss along the wire length.
ETC has nothing to do with the thermo-physical properties of silicon, the bulk and NW silicon properties are the same.
Simple QED applied to < 100 nm NWs shows Planck energies from the UV to the EUV are produced during Joule heat and can be confirmed at the UV level by common UV-VIS spectroscopy.
The significant difference between the shape of ETC curves predicted by simple QED and experiment suggests the experiment should be repeated. Phonon models depending on temperature are not applicable to NWs at temperatures < 300 °K. Only simple QED or other temperature independent ETC models are plausible.
A preliminary Paper is available..
Light from Heat
Although valid for the common heat engine, the Carnot limit of classical physics is not applicable to microscopic heat engines governed by the Planck law of quantum mechanics which denies the atom under high EM confinement the heat capacity to conserve heat by a change in temperature, i.e., a 100% Carnot efficiency is possible, but does not depend on temperature of the cold reservoir. Indeed, heat transfer at the nanoscale by simple QED theory conserves heat by the emission of EM radiation instead of a temperature change. By simple QED, microscopic heat engines remove all thermal energy and directly convert heat to work at 100% Carnot efficiency by emitting EM radiation in the form of non-thermal photons.
Application of simple QED shows converting heat from the ambient 20 °C temperature environment in a 2 cm square silicon surface decorated with a pattern of laser induced 140 nm bottom truncated spherical nanoparticles can produce 50 W light bulbs emitting green light at 580 nm powered only by natural convection.
Conclusions:
The classical Carnot heat engine cannot be 100% efficient as some heat is always loss to the surroundings. 100% conversion of heat QH from the hot reservoir at temperature TH to work W requires a cold reservoir temperature TC of absolute zero.
Microscopic Carnot engines governed by the Planck law avoid the absolute zero requirement of classical physics to allow 100% efficiency by denying the atom under high EM confinement the heat capacity to conserve heat by a change in temperature. Instead, heat is conserved by directly producing work in the emission of EM radiation or photons.
Laser enhanced decoration of 130-140 nm bottom truncated silicon NPs on small 2 cm square silicon films are shown by simple QED to support the fabrication of small 50 W surfaces emitting 580 nm green-light powered only by natural convection from air at 20 °C
The classical notion that in order to turn heat into red-light a metal needs to be heated to approximately 2000 °K is superseded by simple QED under natural convection in air at 20 °C.
The enhanced efficiency of heating the LEDs to 135 °C is caused by the simple QED conversion of heat to work in the form of photons without a need for a cold TC reservoir that does indeed satisfy the second law.
Laser-induced heating of submicron films of silicon nanocrystals embedded in SiO2 separated by pure SiO2 spacers found to increase the radiative emission cannot depend on temperature dependent phonon production as the Planck law denies the existence of temperature at the nanoscale.
CMB Radiation is NOT a Relic of the Big Bang
The CMB evolved from Big Bang models by Gamow. Only in 1965 did Penzias and Wilson discover the microwave radiation coming from space. Dicke and others concluded the microwave radiation was a relic of the Big Bang. Today, the CMB temperature is 2.725 ± 0.00057 K. However, the CMB may have nothing to do with the Big Bang and only be microwave emission from debris in the Oort Cloud of our solar system.
Unlike the disk-like Planetary System in the ecliptic of the Sun, the Oort cloud is spherical allowing the emission of EM radiation observed by Penzias and Wilson to be uniform in all directions. At 10,000 AU, the Oort cloud at 2.725 K varies by ±0.00057 K spread over about 12 AU. Because the Planck law denies atoms at a given temperature below a certain EM confinement wavelength λ the heat capacity to conserve heat by a change in temperature, a debris temperature of 2.725 K is only possible for solar radiation having wavelengths λ> 20,000 microns where atoms have classical and finite heat capacity.
What this means is for λ < 20,000 microns, solar heat is not conserved by a change in temperature, but by creating EM waves standing across debris diameters d > λ /2n, where n is the refractive index of the debris. Taking n = 1.5, the minimum debris diameter d is 7 m that means small to the 8 billion larger asteroids > 5 km reported in the Oort cloud are emitting discrete CMB radiation that appears spotted on WMAP and Planck surveys. Since the CMB of the Big Bang would be uniform and not spotted, the CMB is NOT a relic of the Big Bang
Covid-19: Efficacy of nanoparticles and mRNA vaccines
The CDC approach to the Covid-19 virus was traditional: quickly develop a vaccine that usually takes years, but even if successful in the near term is impossible to implement for the entire World population, let alone unacceptable because of attendant social unrest and economic collapse. On this basis alone, the traditional approach for Covid-19 is not likely to be successful.
Moreover, vaccines typically contain fragments of inactivated viruses. In this regard, the current Pfizer/BioNTech and Moderna vaccines differ in that the inactivated virus is not used, but rather the patient receives an injection of genetic material –mRNA– that encodes the spike protein of Covid-19 virus as the antigen to elicit Covid-19 immunity, the process taking place inside the patient's body.
Since the mRNA molecule is fragile and disintegrates upon entering the cell, the mRNA is dispersed inside ~ 80 nm fatty lipid nanoparticles (NPs). Unfortunately, the NPs naturally emit UVC radiation that inactivates mRNA which makes the concept of mRNA vaccines unworkable. Even so, the mRNA vaccines by Pfizer/BioNTech and Moderna are reported to have a 94.5% efficacy clearly suggesting a mechanism other than mRNA is inactivating the Covid-19.
In this regard, the Covid-19 NP Treatment based on NPs inducing UVC was proposed in mid-2020 as the mechanism to avoid obvious logistical problems in the World-wide delivery of cold storage requirements of Covid-19 vaccines. In the Covid-19 NP Treatment, the UVC need only inactivate a few of the live Covid-19 virus in the patient that then act as the antigen to elicit Covid-19 immunity. But UVC also damages DNA of neurons in the brain. Low NP doses reduce UVC levels to allow correction of DNA damage by repair systems.
But if NP doses are too high, DNA repair systems are overwhelmed and neurological symptoms appear like reported Bell's palsy and allergic reactions. The CDC is requested remove the un-necessary mRNA from vaccines and use the NP Treatment at reduced NP doses. The World population need not be treated, rather only if the patient is tested positive for Covid-19.
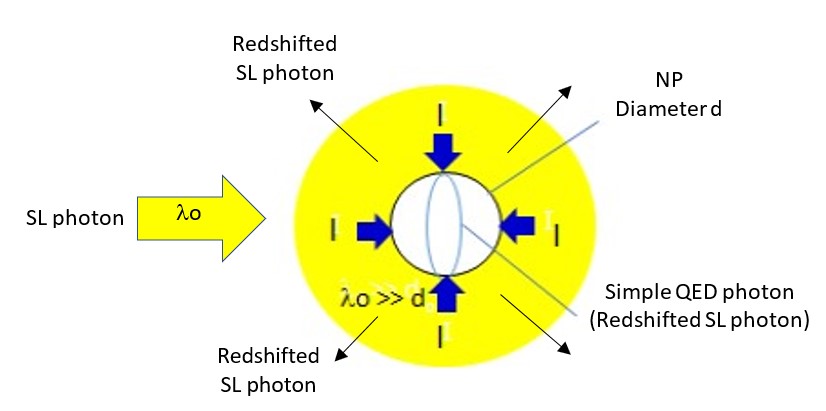
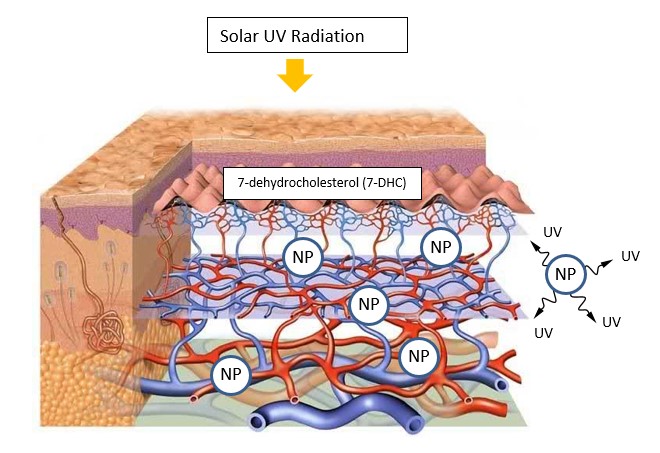
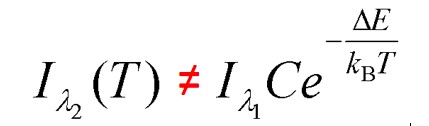
Summary argument:
Since influenza vaccines based on inactivated virus have only 50% efficacy, and since Moderna's Covid-19 mRNA vaccine is the genetic equivalent of an inactivated Covid-19 spike, the efficacy of the Covid-19 mRNA vaccine should be near 50% - not over 90%.
Hence,
The mRNA concept with ~ 80 nm lipid NP carriers emitting UVC is unworkable. But the NP Treatment using NP > 100 nm would emit IR which would not inactivate the mRNA to make the mRNA concept viable, but would reduce the Covid-19 efficacy near 50%
The Abstract of 'Nanoparticles and mRNA Covid-19 efficacy", Paper , and mp4 Video are available.
UVC radiation is known to disinfect Coronavirus in the air or on surrounding surfaces, but not inside body organs.
In this regard, Covid-19 patients diagnosed positive for having the virus in their body are proposed disinfected by a single injection of ~80 nm lipid nanoparticles (NPs) selected to emit UVC radiation. Powered only by body heat, the NPs inactivate at least a few viruses to create the antigens necessary to elicit immunity that removes the remaining virus in the body.
In effect, the UVC Treatment is an 'in vivo' vaccine. In the blood stream, the NPs may enter the brain and damage neurons and DNA, but with brief UVC Treatments the risk of brain damage is expected to be minimal. CDC testing to determine acceptable NP doses is required to avoid neurological problems in Covid-19 patirnts.